01 Jan 2020

Odometry

8059 Blank. beginners' guide to Odometry for VEX Robotics

Overview

Odometry is an algorithm which uses coordinate geometry to determine where and how a robot should move to a location on the field regardless of its current location. This article will discuss the proof of formulas and methods of movements used. The built in v5 PID and okapilib were not used as the built in PID had to be re-tuned in any case as it caused too much wheel slip while the writing our own library gave us more control such as being able to print errors of each motor.

Before reading this document, you should have a basic understanding of trigonometry, arc lengths and PID (PD controller in particular). If you haven o knowledge of PID, I would recommend our beginners’ guide to PID.

Formulas

The basic principle is to take all measurements as arcs. For all encoder measurements, the integrated encoder modules in v5 motors were used. The wheel to be counted was determined by 2 conditions: 1) Either the front or back wheel must be used (Not any wheels in the middle), 2) The wheel that is closer to the centre of gravity (CG).

After further testing, we found that having tracking wheels was the most efficient way to prevent wheel slip. This is where a wheel with a quadrature encoder is mounted on a piece pulled towards the ground, typically using a rubber band.

Tracking wheel CAD example

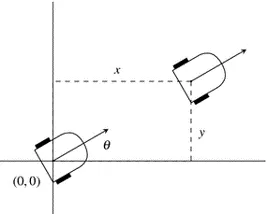
Change in Robot Bearing

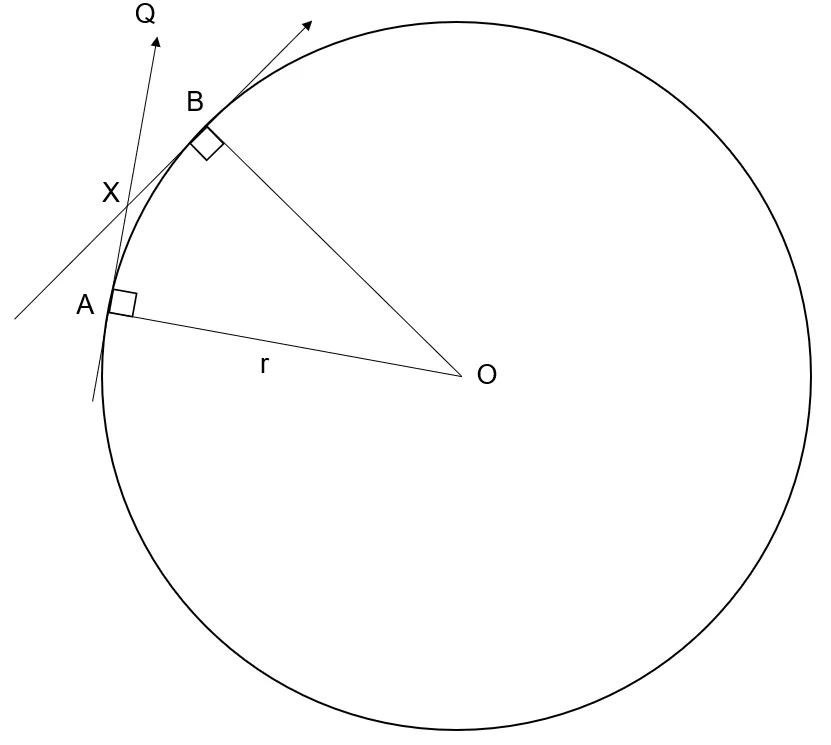
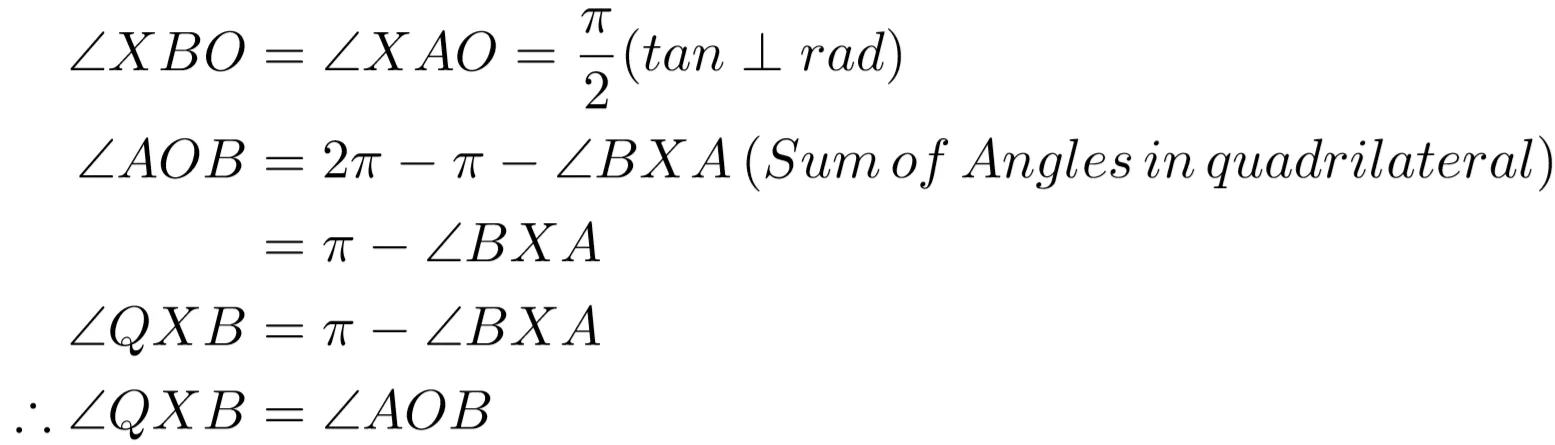
Circle theory diagram for bearing Math calculation for bearing

In the diagram above, the 2 tangents to the circle represent the direction the robot is facing. Therefore, the angle AOB, θ, is the same as the change in bearing in which the robot is facing.

Rotational Movement

Math calculation for rotational movement

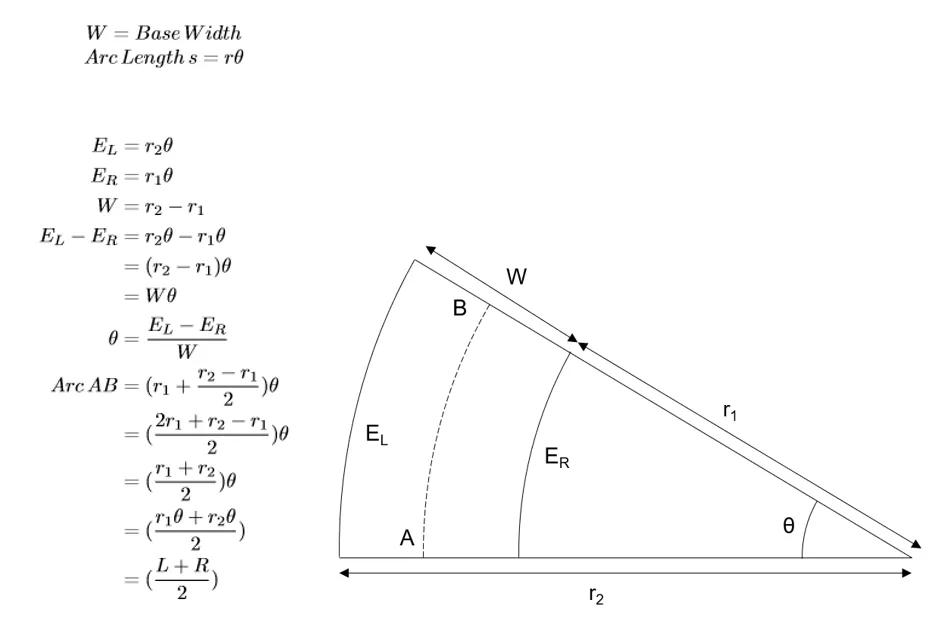
The above equations can be used at any time without resetting the encoders. In the above formulas, EL and ER are taken from the last calibrated angle.

Translational Movement

Circle theory diagram for translational movement Math calculation for translational movement

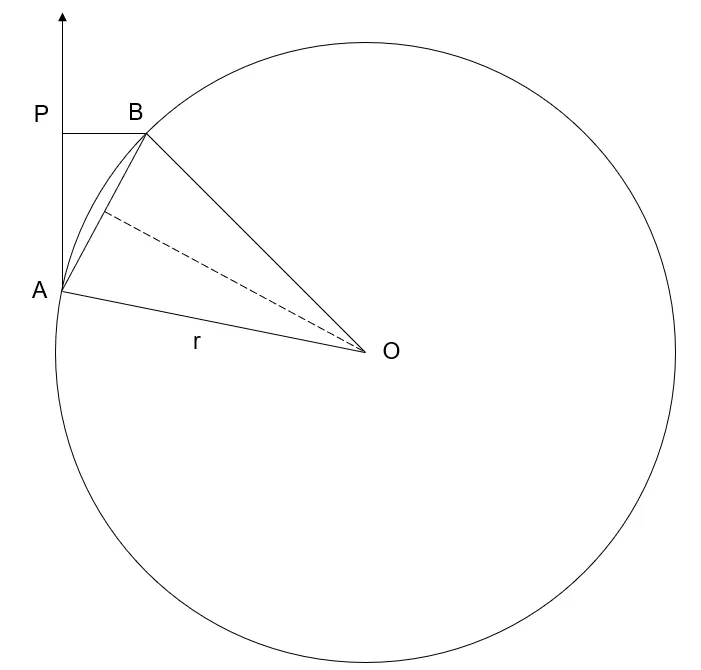
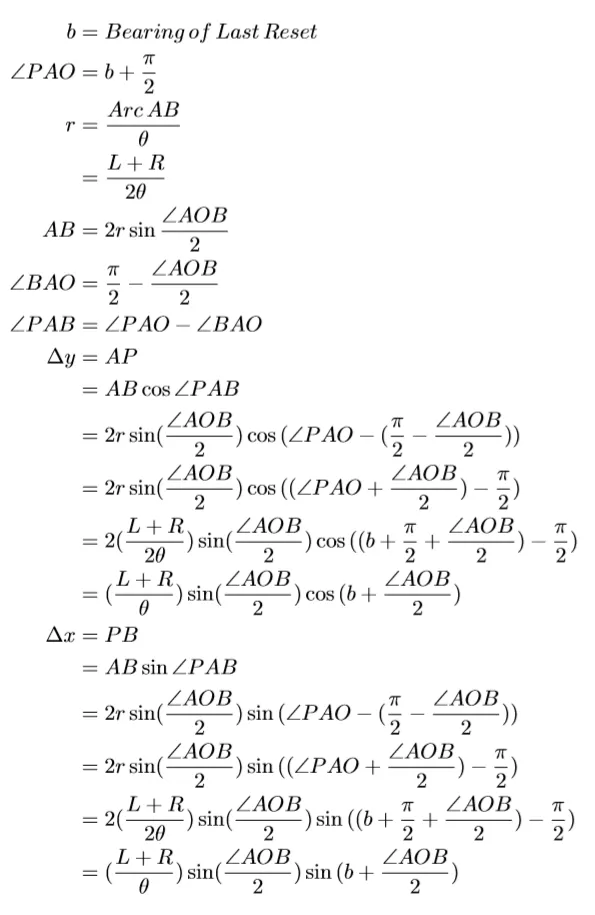
In the example above, b = 0. The 2 formulas above can be used to obtain the translational movement of the robot relative to the last reset position, where ∠PAO is the previous known bearing and ∠AOB is the change in bearing.

Conclusion

With this, we have formulas for both rotational and translational movement. We may also add a third encoder to account for lateral movement. The code for this can be found in 5225A’s code in the GitHub Repository linked below. After implementing odometry, various movement methods may be used. A simple PD control can be used. Do note that with odometry, the possibilities of functions increases. For example, instead of turn to 45 degrees, you can turn to a point using the atan2 function.

Resources